The Vector Product of Vectors
The Vector Product of Vectors: Overview
This topic consists of various concepts like Vector Product Using Determinant,Unit Vector Along the Vector Product of Two Vectors,Right Hand Rule for Vector Product, etc.
Important Questions on The Vector Product of Vectors
If momentum of a particle is given by
a) Find the magnitude of force at any time.
b) Find the angle between momentum and force.
The angle between and is :
What is cross product?
Which of the following is not true about vectors and ?
Find and if and acting along .
The linear velocity of a rotating body is given by is the angular velocity and is the radius vector. The angular velocity of body and this radius vector , then is
Given that are two non-zero vectors, then the value of is,
The angle between two vectors . Then
If then the angle between is
Prove that
Find the cross product .Given and is the distance between two points whose coordinates are (-2, 3, 4) and (1, 2, 3).
If and find the sine of the angle between and .
The vector is a force of newton making an angle of with the displacement of magnitude . Find
(b) The magnitude and direction of the cross product .
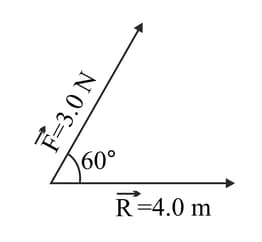
What are the values of the following :
What are the values of the following :
Obtain the condition for the two vectors to be parallel. ?
What is the angle between and ?
What is the condition under which the magnitude of cross product is equal to the dot product ?
What is the condition for parallelism of two vectors ?
If under the condition .What is the angle between them ?
